简单数据结构

复杂度

一个算法的复杂度，会极大影响程序运行的效率，复杂度又分为时间复杂度和空间复杂度，时间复杂度取决于程序运行时基本语句的运算次数，空间复杂度取决于程序运行时所占用的存储空间。复杂度是规模的量级，和数据量的大小成比例，当数据量基数足够大时，算法的优劣就会显示出来。

  • 表示方法：O(n^n),O(n!),O(n),O(1),O(nlogn)等
    评估算法的效率，就需要评估耗费的时间（计算机）和空间（储存占用），主要是相对于输入数据N的比例。

  • 关键点：不同时间复杂度对输入数据量的成长速度是不一样的
    例如：输入数据量为1000时，复杂度为O(n)的算法需要进行1000次基本语句运算，而O(n^2)需要1000000次运算，时间差异是巨大的。因此，解决复杂问题时，要尽可能降低算法的复杂度，以提高程序运行的效率。

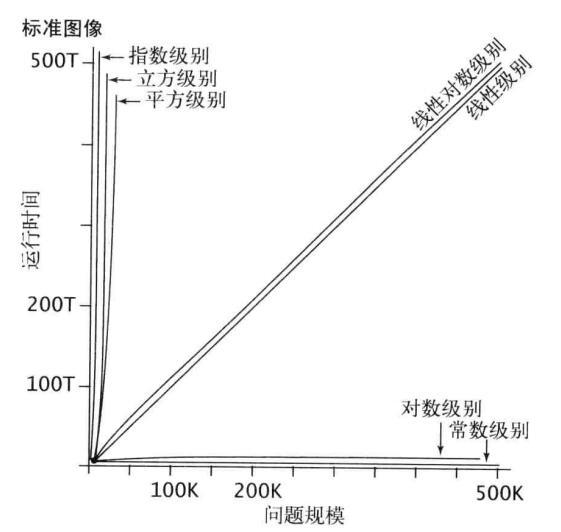
Complexity

  • 简单判断方法：
    1. 数多少个循环嵌套，层数对应于N的次方数
    2. 二分结构一般包含logn

哈希表

  • 哈希表：提供储存Key-Value键值对的数据结构，其中键值均可以为任意类型

  • 特性：储存在哈希表里的数据没有顺序，不可以对哈希表进行排序

  • 基本实现原理：把任意的Key值转换成数字，然后作为数组的下标，再将Value存储在数组下标对应位置上

  • 与数组对比：
    同：
    1. 可以使用下标索引去访问存储的数据
    2. 两者的Value均支持任意类型
    异：
    1. 数组的Key只支持数字，而哈希表的Key支持任意类型
    2. 数组的部分操作，例如在数组中插入数据的操作，时间复杂度为O(n)，而哈希表所有操作（增删改查）时间复杂度都近似于O(1)

操作

增

1
2
3
4
5
6
// 哈希表的建立，键值可为任意类型
HashMap<String, String> nickname = new HashMap<String, String>();

// 用put方法来往哈希表中增加键值对
nickname.put("LiMing", "Ming");
nickname.put("ZiHao", "Wanz");

删

1
2
3
// 用remove方法来移除键值对
nickname.remove("ZiHao");
// nickname.remove("Chen");不会抛出异常

改

1
2
// 改和增一样，用put方法来覆盖键值对
nickname.put("LiMing","Li");

查

1
2
3
4
5
6
7
8
9
// 先用那个containsKey方法判断键值是否存在
if (nickname.containsKey("LiMing")) {
    
    // 存在则用get方法读取，不存在get会返回null
    System.out.println(nickname.get("LiMing"));
}

// 结果
Li

  • 优点：增删改查操作的时间复杂度都近似于O(1),不依赖于插入的顺序，随机访问，查找快，想访问哪个数据就马上访问哪个数据

  • 缺点：牺牲了顺序

栈

  • 栈：一种只能访问最近放入数据的数据结构

  • 特性：
    1. 不可以随机访问，还能按栈堆数据的访问顺序进行，先进后出，后进先出
    2. 除头尾节点之外，每个元素有一个前驱，一个后继
    3. 所有操作的时间复杂度O(1)

操作

推入

1
2
3
4
5
// 新建一个整型栈堆
Stack<Integer> stack = new Stack<Integer>();

// push方法推入数据,放在栈的顶端
stack.push(6);

弹出

1
2
// pop方法取出数据，同时从列表中删除
stack.pop();    //6

查看栈顶数据

1
2
3
4
5
stack.push(4);
stack.push(7);

// peek方法查看栈顶数据，但不移除
stack.peek();   //7

判定是否为空栈

1
stack.isEmpty();    // 返回boolean类型

函数调用栈（递归）

1
2
3
4
5
6
7
8
9
function f1() {
f2();
...
}

function f2(){
f3();
...
}

调用顺序：f1(); -> f2(); ->f3();
调用f1()时，会把f1()的状态装入栈中，再调用f2()

队列

  • 队列：类似于栈的数据结构，区别在于只能访问最早放入的数据

  • 特性：
    1. 不可以随机访问，先进先出，后进后出
    2. 除头尾节点之外，每个元素有一个前驱，一个后继
    3. 所有操作的时间复杂度O(1)

操作

推入

1
2
3
4
5
// 新建一个整型队列
Queue<Integer> queue = new LinkedList<Integer>();

// add方法推入数据
queue.add(6);

弹出

1
2
// poll方法弹出数据
queue.poll();   //6

查看

1
2
3
4
5
queue.add(3);
queue.add(4);

// peek方法查看第一个数据
queue.peek();   //3

判定是否为空队列

1
queue.isEmpty();    // 返回boolean类型